Holzbalkenbemessung nach Eurocode 5

Tragfähigkeitsnachweis nach ÖNORM B 1995-1-1:2015

Materialkennwerte:
Baustoff:
Festigkeitsklasse: *In Europa am häufigsten verwendet.
Sicherheitsfaktoren:
Bemessungssituation γ_m
Nutzungsklasse NKL
Lasteinwirkungsdauer KLED
Systemfestigkeit k_sys
Eingabe:
Breite B [cm]
Höhe H [cm]
Normalkraft N_ed [kN] Druck negativ
Moment M_y,ed [kNm]
Moment M_z,ed [kNm]
Querkraft V_z,ed [kN] bzw. V_z,red
Querkraft V_y,ed [kN] bzw. V_y,red
Torsion M_T,ed [kNm]
Stabilitätsnachweise:	Ja Nein
Biegeknicken
Biegeknicken um y-Achse Knicklänge: s_k,y [m]
Biegeknicken um z-Achse Knicklänge: s_k,z [m]
Biegedrillknicken
wirksame Länge l_ef [m]
Wirksame Länge als Quotient der Stützweite
Lastangriffspunkt

Festigkeits- u. Steifigkeitskennwerte für C16 in N/mm² nach ÖNORM EN 338
Biegefestigkeit	f_m,k=	Zugfestigkeit parallel	f_t,0,k=	Zugfestigkeit rechtwinklig	f_t,90,k=
Druckfestigkeit parallel	f_c,0,k=	Druckfestigkeit rechtwinklig	f_c,90,k=	Schubfestigkeit Torsion	f_v,k=
Rollschubfestigkeit	f_r,k=	E-Modul parallel	E_0,mean=	E-Modul parallel	E_0,05=
E-Modul rechtwinklig	E_90,mean=	E-Modul rechtwinklig	E_90,05=	Schubmodul	G_mean=
Schubmodul	G₀₅=	Rollschubmodul	G_r,mean=	Rohdichte in kg/m³	ρ_k=
Querschnittswiderstände und Beiwerte
Fläche [cm²]	A=	Widerstandsmoment [cm³]	W_y=	Widerstandsmoment [cm³]	W_z=
Höhenbeiwert	k_hz=	Höhenbeiwert	k_hy=	Rissefaktor	k_cr=
Modifikation- beiwert	k_mod=	Teilsicherheits- beiwert	γ_m=	Querschnittsform- beiwert	k_shape=
Torsionsträgh.- moment [cm⁴]	I_T=	Torsionswiders.- moment [cm³]	W_t=	Imperfektions- beiwert	β_c=

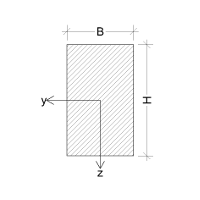
Biegung um die y-Achse

$$\frac{\sigma_{m,y,d}}{f_{m,y,d}}=\frac{\displaystyle\frac{M_{y,ed}}{W_y}}{\displaystyle\frac{f_{m,k}\cdot k_{mod}\cdot k_{hz}\cdot k_{sys}}{\gamma_m}}=$$

Biegung um die z-Achse

$$\frac{\sigma_{m,z,d}}{f_{m,z,d}}=\frac{\displaystyle\frac{M_{z,ed}}{W_z}}{\displaystyle\frac{f_{m,k}\cdot k_{mod}\cdot k_{hy}\cdot k_{sys}}{\gamma_m}}=$$

Doppelbiegung

$$\frac{\sigma_{m,y,d}}{f_{m,y,d}}+k_m\frac{\displaystyle\sigma_{m,z,d}}{\displaystyle f_{m,z,d}}=\frac{\displaystyle\frac{M_{y,ed}}{W_y}}{\displaystyle\frac{f_{m,k}\cdot k_{mod}\cdot k_{hz}\cdot k_{sys}}{\gamma_m}}+0.7\cdot\frac{\displaystyle\frac{M_{z,ed}}{W_z}}{\displaystyle\frac{f_{m,k}\cdot k_{mod}\cdot k_{hy}\cdot k_{sys}}{\gamma_m}}=$$ $$\frac{\sigma_{m,y,d}}{f_{m,y,d}}k_m+\frac{\displaystyle\sigma_{m,z,d}}{\displaystyle f_{m,z,d}}=0.7\cdot\frac{\displaystyle\frac{M_{y,ed}}{W_y}}{\displaystyle\frac{f_{m,k}\cdot k_{mod}\cdot k_{hz}\cdot k_{sys}}{\gamma_m}}+\frac{\displaystyle\frac{M_{z,ed}}{W_z}}{\displaystyle\frac{f_{m,k}\cdot k_{mod}\cdot k_{hy}\cdot k_{sys}}{\gamma_m}}=$$

Zug in Faserrichtung

$$\frac{\displaystyle\sigma_{t,0,d}}{\displaystyle f_{t,0,d}}=\frac{\displaystyle\frac{N_{ed}}A}{\displaystyle\frac{f_{t,0,k}\cdot k_{mod}\cdot k_{hy}\cdot k_{sys}}{\gamma_m}}=$$

Druck in Faserrichtung

$$ \frac{\displaystyle\sigma_{c,0,d}}{\displaystyle f_{c,0,d}}=\frac{\displaystyle\frac{N_{ed}}A}{\displaystyle\frac{f_{c,0,k}\cdot k_{mod}}{\gamma_m}}=$$

Biegung und Zug

$$\frac{\displaystyle\sigma_{t,0,d}}{\displaystyle f_{t,0,d}}+\frac{\sigma_{m,y,d}}{f_{m,y,d}}+k_m\frac{\displaystyle\sigma_{m,z,d}}{\displaystyle f_{m,z,d}}=\frac{\displaystyle\frac{N_{ed}}A}{\displaystyle\frac{f_{t,0,k}\cdot k_{mod}\cdot k_{hy}\cdot k_{sys}}{\gamma_m}}+\frac{\displaystyle\frac{M_{y,ed}}{W_y}}{\displaystyle\frac{f_{m,k}\cdot k_{mod}\cdot k_{hz}\cdot k_{sys}}{\gamma_m}}+k_m\cdot\frac{\displaystyle\frac{M_{z,ed}}{W_z}}{\displaystyle\frac{f_{m,k}\cdot k_{mod}\cdot k_{hy}\cdot k_{sys}}{\gamma_m}}=$$ $$\frac{\displaystyle\sigma_{t,0,d}}{\displaystyle f_{t,0,d}}+k_m\frac{\sigma_{m,y,d}}{f_{m,y,d}}+\frac{\displaystyle\sigma_{m,z,d}}{\displaystyle f_{m,z,d}}=\frac{\displaystyle\frac{N_{ed}}A}{\displaystyle\frac{f_{t,0,k}\cdot k_{mod}\cdot k_{hy}\cdot k_{sys}}{\gamma_m}}+k_m\cdot\frac{\displaystyle\frac{M_{y,ed}}{W_y}}{\displaystyle\frac{f_{m,k}\cdot k_{mod}\cdot k_{hz}\cdot k_{sys}}{\gamma_m}}+\frac{\displaystyle\frac{M_{z,ed}}{W_z}}{\displaystyle\frac{f_{m,k}\cdot k_{mod}\cdot k_{hy}\cdot k_{sys}}{\gamma_m}}=$$

Biegung und Druck

$$\left(\frac{\displaystyle\sigma_{c,0,d}}{\displaystyle f_{c,0,d}}\right)^2+\frac{\sigma_{m,y,d}}{f_{m,y,d}}+k_m\frac{\displaystyle\sigma_{m,z,d}}{\displaystyle f_{m,z,d}}=\left(\frac{\displaystyle\frac{N_{ed}}A}{\displaystyle\frac{f_{c,0,k}\cdot k_{mod}}{\gamma_m}}\right)^2+\frac{\displaystyle\frac{M_{y,ed}}{W_y}}{\displaystyle\frac{f_{m,k}\cdot k_{mod}\cdot k_{hz}\cdot k_{sys}}{\gamma_m}}+k_m\cdot\frac{\displaystyle\frac{M_{z,ed}}{W_z}}{\displaystyle\frac{f_{m,k}\cdot k_{mod}\cdot k_{hy}\cdot k_{sys}}{\gamma_m}}=$$ $$\left(\frac{\displaystyle\sigma_{c,0,d}}{\displaystyle f_{c,0,d}}\right)^2+k_m\frac{\sigma_{m,y,d}}{f_{m,y,d}}+\frac{\displaystyle\sigma_{m,z,d}}{\displaystyle f_{m,z,d}}=\left(\frac{\displaystyle\frac{N_{ed}}A}{\displaystyle\frac{f_{c,0,k}\cdot k_{mod}}{\gamma_m}}\right)^2+k_m\cdot\frac{\displaystyle\frac{M_{y,ed}}{W_y}}{\displaystyle\frac{f_{m,k}\cdot k_{mod}\cdot k_{hz}\cdot k_{sys}}{\gamma_m}}+\frac{\displaystyle\frac{M_{z,ed}}{W_z}}{\displaystyle\frac{f_{m,k}\cdot k_{mod}\cdot k_{hy}\cdot k_{sys}}{\gamma_m}}=$$

Schub V_z in Faserrichtung

$$\frac{\displaystyle\tau_{z,d}}{\displaystyle f_{v,d}}=\frac{\displaystyle\frac{1.5\cdot V_{z,ed}}{A\cdot k_{cr}}}{\displaystyle\frac{f_{v,k}\cdot k_{mod}}{\gamma_m}}=$$

Schub V_y in Faserrichtung

$$\frac{\displaystyle\tau_{y,d}}{\displaystyle f_{v,d}}=\frac{\displaystyle\frac{1.5\cdot V_{y,ed}}{A\cdot k_{cr}}}{\displaystyle\frac{f_{v,k}\cdot k_{mod}}{\gamma_m}}=$$

Schub V_y und V_z in Faserrichtung

$$\left(\frac{\displaystyle\tau_{z,d}}{\displaystyle f_{v,d}}\right)^2+\left(\frac{\displaystyle\tau_{y,d}}{\displaystyle f_{v,d}}\right)^2=\left(\frac{\displaystyle\frac{1.5\cdot V_{z,ed}}{A\cdot k_{cr}}}{\displaystyle\frac{f_{v,k}\cdot k_{mod}}{\gamma_m}}\right)^2+\left(\frac{\displaystyle\frac{1.5\cdot V_{y,ed}}{A\cdot k_{cr}}}{\displaystyle\frac{f_{v,k}\cdot k_{mod}}{\gamma_m}}\right)^2=$$

Torsion

$$\frac{\tau_{tor,d}}{f_{v,d}\cdot k_{shape}}=\frac{\displaystyle\frac{M_{T,ed}}{\displaystyle W_T}}{\displaystyle\frac{f_{v,k}\cdot k_{mod}\cdot k_{shape}}{\gamma_m}}=$$

Schub Q_y und Q_z in Faserrichtung und Torsion

$$\frac{\displaystyle\tau_{tor,d}}{\displaystyle f_{v,d}\cdot k_{shape}}+\left(\frac{\displaystyle\tau_{z,d}}{\displaystyle f_{v,d}}\right)^2+\left(\frac{\displaystyle\tau_{y,d}}{\displaystyle f_{v,d}}\right)^2=\frac{\displaystyle\frac{M_{T,ed}}{\displaystyle W_T}}{\displaystyle\frac{f_{v,k}\cdot k_{mod}\cdot k_{shape}}{\gamma_m}}+\left(\frac{\displaystyle\frac{1.5\cdot V_{z,ed}}{A\cdot k_{cr}}}{\displaystyle\frac{f_{v,k}\cdot k_{mod}}{\gamma_m}}\right)^2+\left(\frac{\displaystyle\frac{1.5\cdot V_{y,ed}}{A\cdot k_{cr}}}{\displaystyle\frac{f_{v,k}\cdot k_{mod}}{\gamma_m}}\right)^2=$$

Biegeknicken um die Y-Achse

Trägheitsradius: $$i_y=\sqrt{\frac{I_y}A}=$$ cm
Schlankheit: $$\lambda_y=\frac{s_{k,y}}{i_y}=$$
bezogene Schlankheit: $$\lambda_{rel,y}=\frac{\lambda_y}\pi\cdot\sqrt{\frac{f_{c,0,k}}{E_{0,05}}}=$$

Beiwert: $$k_y=0.5\cdot\left[1+\beta_c\cdot\left(\lambda_{rel,y}-0.3\right)+\lambda_{rel,y}^2\right]=$$
Knickbeiwert: $$k_{c,y}=\frac1{k_y+\sqrt{k_y^2-\lambda_{rel,y}^2}}=$$ $$\frac{\displaystyle\sigma_{c,0,d}}{\displaystyle k_{c,y}\cdot f_{c,0,d}}+\frac{\sigma_{m,y,d}}{f_{m,y,d}}+k_m\frac{\displaystyle\sigma_{m,z,d}}{\displaystyle f_{m,z,d}}=\frac{\displaystyle\frac{N_{ed}}A}{\displaystyle\frac{k_{c,y}\cdot f_{c,0,k}\cdot k_{mod}}{\gamma_m}}+\frac{\displaystyle\frac{M_{y,ed}}{W_y}}{\displaystyle\frac{f_{m,k}\cdot k_{mod}\cdot k_{hz}\cdot k_{sys}}{\gamma_m}}+k_m\cdot\frac{\displaystyle\frac{M_{z,ed}}{W_z}}{\displaystyle\frac{f_{m,k}\cdot k_{mod}\cdot k_{hy}\cdot k_{sys}}{\gamma_m}}=$$

Biegeknicken um die Z-Achse

Trägheitsradius: $$i_z=\sqrt{\frac{I_z}A}=$$ cm
Schlankheit: $$\lambda_z=\frac{s_{k,z}}{i_z}=$$
bezogene Schlankheit: $$\lambda_{rel,z}=\frac{\lambda_z}\pi\cdot\sqrt{\frac{f_{c,0,k}}{E_{0,05}}}=$$

Beiwert: $$k_z=0.5\cdot\left[1+\beta_c\cdot\left(\lambda_{rel,z}-0.3\right)+\lambda_{rel,z}^2\right]=$$
Knickbeiwert: $$k_{c,z}=\frac1{k_z+\sqrt{k_z^2-\lambda_{rel,z}^2}}=$$ $$\frac{\displaystyle\sigma_{c,0,d}}{\displaystyle k_{c,z}\cdot f_{c,0,d}}+k_m\frac{\sigma_{m,y,d}}{f_{m,y,d}}+\frac{\displaystyle\sigma_{m,z,d}}{\displaystyle f_{m,z,d}}=\frac{\displaystyle\frac{N_{ed}}A}{\displaystyle\frac{k_{c,z}\cdot f_{c,0,k}\cdot k_{mod}}{\gamma_m}}+k_m\cdot\frac{\displaystyle\frac{M_{y,ed}}{W_y}}{\displaystyle\frac{f_{m,k}\cdot k_{mod}\cdot k_{hz}\cdot k_{sys}}{\gamma_m}}+\frac{\displaystyle\frac{M_{z,ed}}{W_z}}{\displaystyle\frac{f_{m,k}\cdot k_{mod}\cdot k_{hy}\cdot k_{sys}}{\gamma_m}}=$$

Biegedrillknicken

effektive Länge l_ef = cm

kritische Biegespannung: $$\sigma_{m,crit}=\frac{M_{y,crit}}{W_y}=\frac{\pi\cdot\sqrt{E_{0,05}\cdot I_z\cdot G_{0,05}\cdot I_T}}{l_{ef}\cdot W_y}=$$ N/mm²

kritische Biegespannung: $$\sigma_{m,crit}=\frac{0.78\;\cdot b^2}{h\cdot l_{ef}}\cdot E_{0,05}=$$ N/mm²

bezogene Kippschlankheitsgrad: $$\lambda_{rel,m}=\sqrt{\frac{f_{m,k}}{\sigma_{m,crit}}}=$$

Kippbeiwert: $$k_{crit}=$$

Kippbeiwert: $$k_{crit}=1.56-0.75\cdot\lambda_{rel,m}=$$

Kippbeiwert: $$k_{crit}=\frac1{\lambda_{rel,m}^2}=$$

Knickbeiwert: k_c,y = k_c,z = $$\frac{\displaystyle\sigma_{c,0,d}}{\displaystyle k_{c,y}\cdot f_{c,0,d}}+\frac{\sigma_{m,y,d}}{k_{crit}\cdot f_{m,y,d}}+\left(\frac{\displaystyle\sigma_{m,z,d}}{\displaystyle f_{m,z,d}}\right)^2=\frac{\displaystyle\frac{N_{ed}}A}{\displaystyle\frac{k_{c,y}\cdot f_{c,0,k}\cdot k_{mod}}{\gamma_m}}+\frac{\displaystyle\frac{M_{y,ed}}{W_y}}{\displaystyle\frac{k_{crit}\cdot f_{m,k}\cdot k_{mod}\cdot k_{hz}\cdot k_{sys}}{\gamma_m}}+\left(\frac{\displaystyle\frac{M_{z,ed}}{W_z}}{\displaystyle\frac{f_{m,k}\cdot k_{mod}\cdot k_{hy}\cdot k_{sys}}{\gamma_m}}\right)^2=$$ $$\frac{\displaystyle\sigma_{c,0,d}}{\displaystyle k_{c,z}\cdot f_{c,0,d}}+\left(\frac{\sigma_{m,y,d}}{k_{crit}\cdot f_{m,y,d}}\right)^2+\frac{\displaystyle\sigma_{m,z,d}}{\displaystyle f_{m,z,d}}=\frac{\displaystyle\frac{N_{ed}}A}{\displaystyle\frac{k_{c,z}\cdot f_{c,0,k}\cdot k_{mod}}{\gamma_m}}+\left(\frac{\displaystyle\frac{M_{y,ed}}{W_y}}{\displaystyle\frac{k_{crit}\cdot f_{m,k}\cdot k_{mod}\cdot k_{hz}\cdot k_{sys}}{\gamma_m}}\right)^2+\frac{\displaystyle\frac{M_{z,ed}}{W_z}}{\displaystyle\frac{f_{m,k}\cdot k_{mod}\cdot k_{hy}\cdot k_{sys}}{\gamma_m}}=$$